Compared with other sort algorithms, quick sort is more popular since it’s not difficult to implement, works well for various input data, and is substantially faster than any other sorting algorithms in typical applications.
Divide and conquer
Divide and conquer is a way to break complex problems into two or smaller sub-problems of the same or related type and then combine the answers to solve the original problem. In simple terms, divide and conquer can be done in 3 steps:
- divide (into sub-problems)
- conquer (by solving the sub-problems)
- combine (the answers to solve the original problem)
There are two aspects to this concept that require attention:
- the way to recursively divide the original problem
- the base case
Overview of quick sort
Quick sort is a fast sorting algorithm based on the divide and conquers approach to sort the list. It works by selecting a Pivot element from the array and partitioning the other elements into two sub-arrays according to whether they are less than or greater than the pivot. The sub-arrays are then sorted recursively.
As we discussed, the process of quick sort can be divided into 3 steps:
- Divide an array into sub-arrays by selecting a pivot element. At this moment, we should keep the elements less than the pivot on the left side and elements greater than the pivot on the right side of the pivot.
- Divide the left and right sub-arrays using the same approach, continuing this process until each sub-arrays contains a single element.
- Combine elements to form a sorted array.
According to above procedure, we can implement the quick sort algorithm as the following code:
// lo: low bounds of the array
// hi: high bounds of the array
fun quickSort(array, lo, hi):
if (hi <= lo) return
set pivot = partition(array, lo, hi)
quickSort(array, lo, pivot - 1)
quickSort(array, pivot + 1, hi)As you can see, quick sort also is a recursive sorting algorithm, just like merge sort. But the difference is quick sort does the two recursive calls after working on the whole array. And merge sort will divide the original array in half; for quick sort, the position of the pivot depends on the array’s contents.
Partition
The key to the quick sort is the partition process. There are some different ways to implement this process, but we will follow the general strategy:
- Chose the first position of array as the partitioning item
- Scan the array from left end until finding an item greater/equal than the partiotioning item.
- Scan the array from right end until finding an item less/equal than the partiotioning item.
- Exchange the item of two pointers, continuing in this way until i and j cross.
- Exchange the partiotioning item with the rightmost item of the left sub-array.
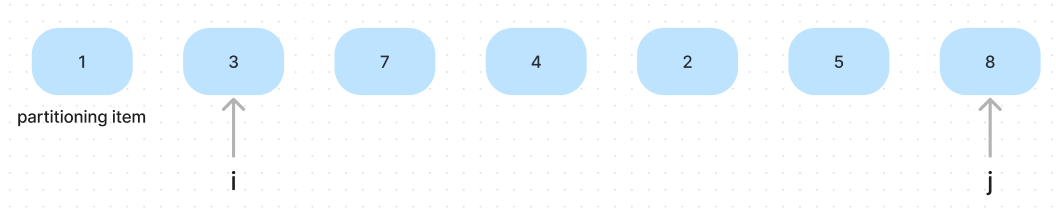
According to the steps and the diagram, we have the following pseudo-code:
// lo: low bounds of the array
// hi: high bounds of the array
fun partition(array, lo, hi):
set i = lo
set j = hi + 1
set pivot = array[lo]
while (true):
while (a[++i] < pivot):
// right checking
if (i == hi): break
while (a[--j] > pivot):
// left checking
if (j == lo): break
// two pointers cross
if (i >= j): break
exchange the array[i] with array[j]
// Only happen when i >= j
// i = j, it's equal to exchange with i or j
// i > j, a[i] never smaller than pivot
exchange the pivot with array[j]
return jWorest case
As we can see, the pivot determine where the algorithm will splice the original array into two sub-arrays. It will affect the performance of the algorithm significantly.
If the original array is sorted, the pivot lies at an extreme end of the sorted array. This means one sub-array is always empty, and another contains n - 1 elements. In other words, the algorithm is called only on this sub-array.
So it’s better to shuffle the array before sorting it. It can eliminate the impact of input on algorithm performance.
fun quickSort (array):
shuffle the array
push positive infinity to the end of the array
sort(array, 0, array.size - 1)
pop the end item of the array
fun sort(array, lo, hi):
if (hi <= lo) return
val povit = partition(array, lo, hi)
sort(array, lo, povit - 1)
sort(array, povit, hi)
// ...Bounds checking
We have bounds checking to prevent pointers walk out of the scope when the smallest or largest item in the array is the pivot item. But these two checkings are redundant.
For the left checking, we know the array[lo] is the pivot, so when the j pointer walks to the left bounds, it’s never less than the pivot since it’s never less than itself.
For the right checking, when the know i pointer only scans the items smaller than pivot, so we can add a super large item at the end of the array, it will limit the pointer’s movement.
So the code will be:
fun quickSort (array):
shuffle the array
push positive infinity to the end of the array
sort(array, 0, array.size - 1)
pop the end item of the array
fun sort(array, lo, hi):
if (hi <= lo) return
val povit = partition(array, lo, hi)
sort(array, lo, povit - 1)
sort(array, povit, hi)
fun partition(array, lo, hi):
set i = lo
set j = hi + 1
set v = a[lo]
while true:
while a[++i] < v: empty
while a[--j] > v: empty
if i >= j: break
exchange array[i] and array[j]
exchange array[lo] and array[j]
return jComplexity
| Best time complexity | |
| Worst time complexity | |
| Average time complexity | |
| Space complexity | |
| Stability | No |
Additional
If you are interested in a mathematical proof of the algorithm, you can read this article
Reference
- Algorithms 4th, 2.3 quicksort
- Quicksort Algorithm