Overview
Symbol table (also called a dictionary) is a common data structure, and many major programming languages have built-in implementations. The idea of a symbol table is also pretty straightforward, create a data structure, and store the key-value pairs in it. We can search the key to get the value, just like we use a real dictionary. Benefit from how it’s implemented; the speed of searching is fast.
We will start from the conceptions of the symbol table and discuss its API; by the way, we’ll talk a little bit about some intuitive but inefficient implementations: Unordered linked list and ordered array.
We always want to use more efficient data structures. Thus we will discuss the Binary search tree, a widely used and efficient implementation of the symbol table. Similarly, we’ll also start from the definition and API. After that, since it’s a tree actually, so it’s vital to know how to traverse it, and we’ll also implement a useful method: rank operation. Of course, to manipulate a data structure in the real system, we need functionality that lets us put new elements into and remove elements from it; we will discuss this part at the end of this section.
Finally, we will study the relationship between binary search tree and quick sort. It can help us understand them deeply.
Symbol tables
The symbol table is a structure for organizing information. In most scenarios, the information will be key-value pairs. On the one hand, we can say the functionality of the symbol table is to store the relationship between key and value; on the other hand, the key can be seen as the unique identifier of the value, as you can see in many programming language built-in implementation of the symbol table, they always require the key should be unique; otherwise, the old value will be overwritten by the new value.
The following is an example of a symbol table:
| Character (key) | Description (value) |
|---|---|
| Spike Spiegel | Spike Spiegel is a tall, lean, and slightly muscular 27-year-old bounty hunter born on Mars |
| Jet Black | Known on his home satellite as the “Black Dog” for his tenacity, Jet Black is a 36-year-old former cop from Ganymede (a Jovian satellite) and acts as Spike’s foil during the series |
| Faye Valentine | Faye Valentine is one of the members of the bounty hunting crew in the anime series Cowboy Bebop |
According to the discussion above, we have the following interface design.
interface SymbolTable(K, V)<K: Comparable<K>, V> {
fun get(k: K): V?
fun put(k: K, v: V)
fun delete(k: K)
fun contains(k: K): Boolean
fun isEmpty(): Boolean
}Generally, we need the ability to add, get and delete elements from the data structure. Also, checking if an element exists and the data structure instance is empty is useful for the client.
Inefficient implementations
The most straightforward way is using the unordered linked list. Each node has three fields: key, value, and the pointer to the next node. The get is straightforward; just traversal the linked list and find the given key. But the problem is, in the worst case of the get method, we need to traverse the entire list, and it requires comparisons. On average, it requires comparisons. Similarly, we need to check if the given key exists in the linked list when the client adds a new element; that said, the comparisons for this process will be .
Another opposite way is to use the ordered array. It’s straightforward to search for a given key in an ordered array. Just traverse it! Going further, since it’s an ordered array, we can use the binary search to decrease time complexity. It can make both the average and worst-case number of comparison . But this is an array after all; in other words, when inserting a new element, we need to move all the following elements. Consequently, the insertion cost is still in the worst case and on average.
Binary search tree
A binary search tree (BST) is a widely used data structure for implementing a symbol table. It combines the flexibility of insertion in linked lists with the efficiency of searching in an ordered array. A binary search tree is like a linked list Pro, but the nodes in the BST contain more information than those in the linked list — fields containing the key, some associated data, and two pointers to other nodes. The following is the data structure of the node.
data class Node<K, V)(val key: K, var value: V) {
var left: Node<K, V>? = null
val right: Node<K, V>? = null
}And to be a binary search tree, it has to follow these properties:
- The left sub-tree of a node contains only nodes with keys lesser than the node’s key
- The right sub-tree of a node contains only nodes with keys greater than the node’s key
- The left and right sub-tree each must also be a binary search tree
A binary search tree is a special tree, or one step more, a special type of graph. When we describe some tree components, we will use some specific vocabulary to describe them. You can find most of them on this website. We will just discuss two important terminologies: symmetric order and perfectly balanced.
If every node’s key is both larger than all keys in its left sub-tree and smaller than all in its right sub-tree, we say the tree is in symmetric order. If every non-left node has a left and right child and every leaf node is at the same level, we say the tree is perfectly balanced.
For a reasonably balanced tree of nodes, if we note its height is , we have node of level ; nodes of level , etc. Thus we have:
Since we have a formula for finite geometric series:
Here, , we have:
Solving in the above for , we have:
Thus we can say the height is .
Tree traversal
As we all know, we have three different ways of traversing the binary tree, and those are in-order traversal, post-order traversal, and pre-order traversal. We will discuss them based on a normal binary tree.
In-order traversal
To implement an in-order traversal on a binary tree, we need:
- visit all of the nodes in the sub-tree topped by ’s left child first
- visit itself
- visit all of the nodes in the sub-tree topped by ’s right child
The following is the code:
typealias Visit = (node: Node<K, V>) -> Void
fun <K, V> traverse(node: Node<K, V>?, visit: (node: Visit) {
if (node == null) return
traverse(node.left, visit)
visit(node)
traverse(node.left, visit)
}Interestingly, the result of in-order traversal on a binary search tree is a sequence of increasing orders.
Post-order traversal
To implement a post-order traversal on a binary tree, we need:
- visit all of the nodes in the sub-tree topped by ’s left child first
- visit all of the nodes in the sub-tree topped by ’s right child
- visit itself
The following is the code:
typealias Visit = (node: Node<K, V>) -> Void
fun <K, V> traverse(node: Node<K, V>?, visit: (node: Visit) {
if (node == null) return
traverse(node.left, visit)
traverse(node.left, visit)
visit(node)
}Pre-order traversal
To implement a pre-order traversal on a binary tree, we need:
- visit itself
- visit all of the nodes in the sub-tree topped by ’s left child first
- visit all of the nodes in the sub-tree topped by ’s right child
The following is the code:
typealias Visit = (node: Node<K, V>) -> Void
fun <K, V> traverse(node: Node<K, V>?, visit: (node: Visit) {
if (node == null) return
visit(node)
traverse(node.left, visit)
traverse(node.left, visit)
}Rank operations
According to the discussion above, it’s easy to know the smallest key in the tree is the most left node of the tree and the largest key is the most right. But how to get the 10th node? Or, suppose we use the binary search tree to hold the runners’ names and use the time of the runners in a race to be the key. Can we find the rank associated with a given time scope?
Let’s consider this scenario the minimum key has rank 0, the next smallest has rank 1, and so on. In doing so, we can infer the rank of any key is equal to the number of keys in the tree less than that key. Thus, we can implement a function to find the rank of any given key:
fun rank(node: Node<K, V>, key: K): Int {
if (node == null) return 0
val gap: Int = key.compareTo(node.key)
return if (gap > 0) {
1 + size(node.left) + rank(node.right, key)
} else if (gap < 0) {
rank(node.left, key)
} else {
size(node.left)
}
}The size procedure will return the number of nodes in the sub-tree of a given node.
Of course, following the logic, we can implement the opposite procedure, which is to find the key of a given rank.
fun key(node: Node<K, V>, rank: Int): K {
if (node == null) return null
val numOfLeftTree: Int = size(n.size)
return if (numOfLeftTree > rank) {
// current node's rank is larger than the given rank
// thus we nned to choose the left sub-tree
key(node.left, rank)
} else if (numOfLeftTree < rank) {
// Jump to right sub-tree, we don't num of left tree and current tree
// Suppose the given rank is 12, and current node's rank is 10
// Note that 12th is also the 2ed after 10th
key(node.right, rank - numOfLeftTree - 1)
} else {
// Here it is!
return node
}
}Get & put methods
As one kind of implementation of the symbol table, the binary search tree must be able to store key-value pairs. To implement those, we need to implement these methods in the interface:
interface SymbolTable(K, V)<K: Comparable<K>, V> {
fun get(k: K): V?
fun put(k: K, v: V)
// ...
}As you can see in the definition of the interface, the upper bound of the generic key Key is the Comparable<T>. This, of course, allows us to compare the keys in the binary search tree with any key for which we might be searching. Based on this design, we can take advantage of the properties of the binary search tree to implement the get method. Consider the following example:
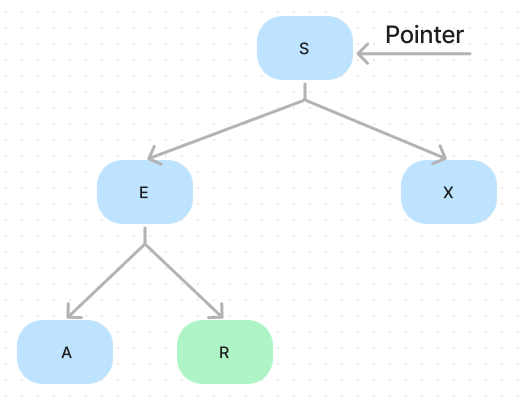
Suppose we seek the node with the key R, the green node. We know the entire binary search tree has only one reference to the node S identified as root. To seek R, we need to start from the root node. Thus, we create a pointer and point it to the root node S.
Compare the node’s key pointed by the pointer with what we want, noting that . Since in the binary search tree, the nodes’ key in the left sub-tree is smaller than the current topped node’s key, we can infer that R is never in the right sub-tree. Thus we make the pointer point to the E. Continue the above logic; the pointer will point to the right sub-tree of E. We find, at that moment, it is equal to our target. We’re done.
But at this point, we immediately think, if the key we are searching for is not in the binary search tree, how to know that? Well, it’s pretty easy. Suppose we seek the node with the key F; after going through similar steps as above, the pointer points to node R. We find the R is a leaf node, which means it has no sub-tree, and the value left and right are both null. At that moment, we can say, F is not in the current binary search tree. By the way, this is the worst case of get methods.
According to the discussion above, we can implement the get:
fun get(node: Node<K, V>?, key: K): V? {
if (node == null) return null
val gap: Int = key.compareTo(node.key)
return if (gap > 0) {
get(node.right, key)
} else if (gap < 0) {
get(node.left, key)
} else {
node.value
}
}It’s easy to know that the get method follows one path of the binary search tree when it seeks the given key. Thus the comparisons’ number is one more than the depth of the given node if it exists in the binary search tree, and the worst-case number of comparison s is one more than the tree’s height. For a perfectly balanced binary search tree of nodes, the comparison number will be .
Similar to the get method, we must find the location for the insertion by comparing each node’s key with the given key; thus, most codes of put are the same as get. But the get method has two base cases. The first is that when the position we seek already has a node, we need to update the value of that node. This logic also follows the property of the symbol table: uniquid key. The second is that when the pointer reaches the leaf node but still hasn’t found the position, we need to create a new node, put it under the current leaf node, and make it follow the property of the binary search tree. The following is the code:
fun put(node: Node<K, V>?, key: K, value: V): Node<K, V> {
if (node == null) {
size++
return Node(key, value)
}
val gap: Int = key.compareTo(node.key)
if (gap > 0) {
// link the tree's ndoes
node.right = put(node.right, key, value)
} else if (gap < 0) {
node.left = put(node.left, key, value)
} else {
node.value = value
}
return node
}Similar to the put method, the comparison cost for a perfectly balanced tree of nodes.
Finally, we noticed that binary search trees’ get and put speed is extremely fast. :tada:
Hibbard deletion
We already implemented the put to insert new elements into the binary search tree, but how do we delete them? Like the heap, after deleting, we must keep the new tree as a binary search tree. One efficient way to do this was implemented by Thomas Hibbard in 1962. The idea is to swap the node to be deleted with its successor. The successor is the following largest key in the tree; in other words, it’s the minimum key in the right sub-tree of the node to be deleted.
To implement this procedure, we need to implement delMin first. This function will delete the minimum key in the right sub-tree of a given node. Since the elementary property of the binary search tree is for any given node, the nodes larger than the given node are in the right sub-tree, and the nodes smaller than the given node are in the left sub-tree. Thus we can choose the left sub-tree recursively until the value of the left pointer is null. If the current node has a right sub-tree, it should be the left sub-tree of the previous node since all nodes are smaller than the previous node.
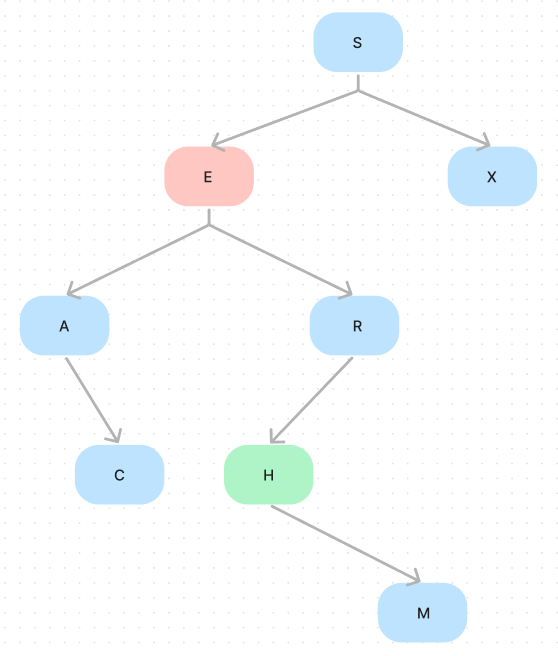
Suppose we want to use the procedure delMin for node E. The minimum node of E is H (Since it doesn’t have a left sub-tree). Thus we can delete it, but after that, we need to process M, which is the right sub-tree of H. Note that since M is in the right sub-tree, it’s bigger than H. But since H is in the left sub-tree of R, all node in this left sub-tree is smaller than R. In summary, M will be the left tree of R. The following is the code:
fun delMin(n: Node<K, V>) {
if (n.left == null) return n.right
n.left = delMin(n.left)
n.count = 1 + size(n.left) + size(n.right)
return n
}With this procedure, we can understand the Hibbard deletion easily.
The first step of the deletion is to find the node we want to delete. It’s easy since we have implemented it in the previous methods. The second step is to find the successor of the given node, which is in the right sub-tree. Note that the successor is the minimum node in the right sub-tree; in other words, all node in the right sub-tree is larger than the successor. Thus we can put it in the same position as the given node. After this step, we will have two successor nodes, as shown in the following diagram (H is the successor of E).
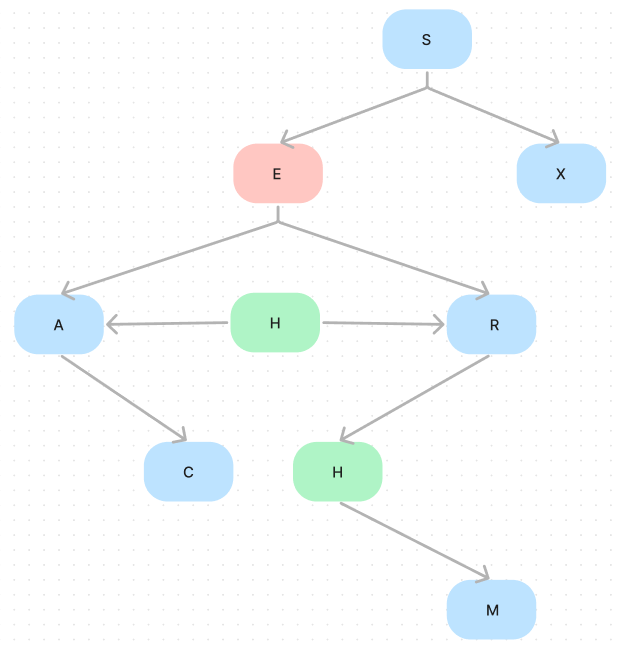
So we can invoke delMin on the given node and delete that original successor. And then delete the given node.
The following is the code:
fun delete(node: Node<K, V>, key: K) {
if (node == null) return null
val gap: Int = key.compareTo(node.key)
if (gap > 0) {
n.right = delete(n.right, key)
} else if (gap < 0) {
n.left = delete(n.left, key)
} else {
// Since the given node doesn't have successor
// Return the left sub-tree and this does NOT destroy the BST
if (node.right == null) return n.left
val temp: Node<K, V> = node
// Find the successor and put it in the given key's position
node = min(temp.right)
node.right = deleteMin(t.right)
node.left = t.left
}
node.count = size(node.left) + size(node.right) + 1
return node
}The connection between BST and quick sort
After we understand the mechanism of the binary search tree, for a perfectly balanced binary tree, the inserting procedure needs times comparison to insert a new node. But worst case, if we insert a series of ordered numbers, each number must compare with all previous numbers. In general, we have:
Thus we can say the comparison required to insert elements in order is . To prevent this scenario, we can shuffle the order of elements randomly. You may notice it now at this point. Yep, same situation we encountered when we discussed the quick sorting!
We have an array with the same number of comparisons when we insert them into an empty binary search tree as the number of comparisons of another array when we invoke a quick sorting algorithm. Of course, another array has the same elements. One example is C, B, A, G, F, D, E and C, A, G, E, D, B, F.